ProVerb
Prognosewerkzeuge für das mechanische Verhalten von Beton über lange Zeiträume zur Sicherheitsanalyse von Verschlusssystemen für Endlagerstätten
Engl.:
Prediction tools for the mechanical behaviour of concrete over long time spans for the safety analysis of locking systems for final repositories
Info
- Project Term: 01.04.2018 - 30.09.2021
- Project Partner: University of Stuttgart (Institute for Nonlinear Mechanics; Materials Testing Institute); BGE Technology GmbH (associated partner)
- Form of Funding: KMU innovativ cooperation
- Funding Code: 01 IS 17096A
- Funding Body: BMBF
- Executing Organization: DLR PT-SW
Project Partners
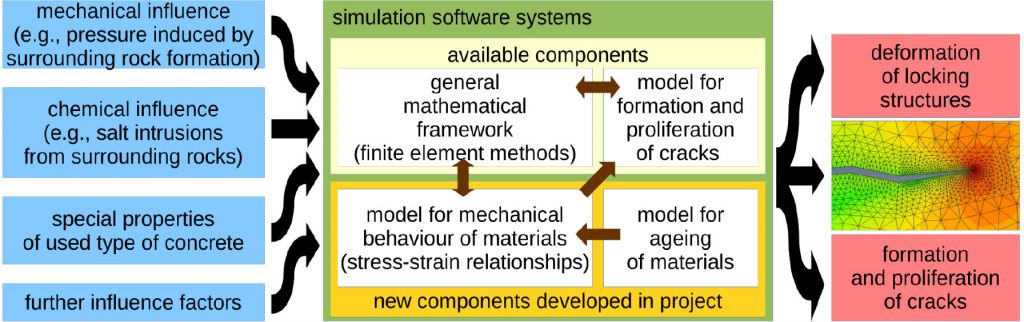
The verification of the safety of a final repository for radioactive waste requires, among others, to provide computational evidence that the locking systems for the storage caverns (typically, walls made of concrete) can guarantee a tight enclosure of the radioactive material for one million years. To obtain such evidence, it is necessary to develop new material models for concrete that remain valid over such a time span which is larger than those usually considered by many orders of magnitude.
Determination of material properties
Creep test with concrete specimen
(Photo: M. Kovalenko)
Fractional Zener model in Maxwell form
Creep test for concrete: measured hydrostatic strains and results of corresponding simulations
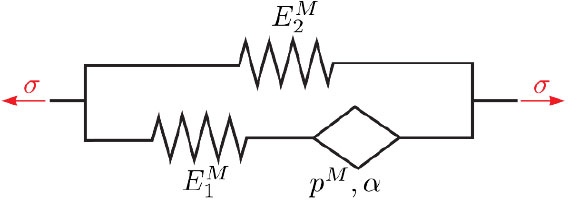
The verification of the safety of a final repository for radioactive waste requires, among others, to provide computational evidence that the locking systems for the storage caverns (typically, walls made of concrete) can guarantee a tight enclosure of the radioactive material for one million years. To obtain such evidence, it is necessary to develop new material models for concrete that remain valid over such a time span which is larger than those usually considered by many orders of magnitude. In particular, the fact that concrete exhibits viscoelastic behaviour cannot be neglected any more. An appropriate mathematical tool for such models is the concept of differential operators of fractional (i.e., non-integer) order. Once these models have been derived, numerical methods for handling the associated model equations must be constructed, implemented and integrated into the existing framework of general purpose finite element software packages.
Link:
https://www.inm.uni-stuttgart.de/research_nonlinear_mechanics/project_hinze_schmidt_proverb/
Publications
- K. Diethelm: Fundamental Approaches for the Numerical Handling of Fractional Operators and Time-Fractional Differential Equations. In G. E. Karniadakis (Ed.): Handbook of Fractional Calculus with Applications, Vol. 3: Numerical Methods. De Gruyter, Berlin, 2019, pp. 1-22, DOI 10.1515/9783110571684-001.
- K. Diethelm, R. Garrappa & M. Stynes: Good (and Not So Good) Practices in Computational Methods for Fractional Calculus. Mathematics 8 (2020), Article No. 324, DOI 10.3390/math8030324.
- K. Diethelm, R. Garrappa, A. Giusti & M. Stynes: Why Fractional Derivatives with Nonsingular Kernels Should Not Be Used. Fract. Calc. Appl. Anal. 23 (2020), 610-634, DOI 10.1515/fca-2020-0032.
- M. Hinze, A. Schmidt & R. I. Leine: Numerical Solution of Fractional-order Ordinary Differential Equations Using the Reformulated Infinite State Representation. Fract. Calc. Appl. Anal. 22 (2019), 1321-1350, DOI 10.1515/fca-2019-0070.
- M. Hinze, A. Schmidt & R. I. Leine: Numerical Simulation of Fractionally Damped Mechanical Systems Using Infinite State Representation. Proc. 2019 International Conference on Fractional Calculus Theory and Applications, Bourges, France
- M. Hinze, A. Schmidt & R. I. Leine: The Direct Method of Lyapunov for Nonlinear Dynamical Systems with Fractional Damping. Nonlinear Dynam. 102 (2020), 2017-2037, DOI 10.1007/s11071-020-05962-3.
- M. Hinze, A. Schmidt & R. I. Leine: Lyapunov Stability of a Fractionally Damped Oscillator with Linear (Anti-) Damping. Internat. J. Nonlin. Sci.Numer. Simul. 21(5) (2020), 425-442, DOI 10.1515/ijnsns-2018-0381.
- M. Hinze, A. Schmidt & R. I. Leine: Finite Element Formulation of Fractional Constitutive Laws Using the Reformulated Infinite State Representation. Fractal Fract. 5(3) (2021), Article No. 132, DOI 10.3390/fractalfract5030132.
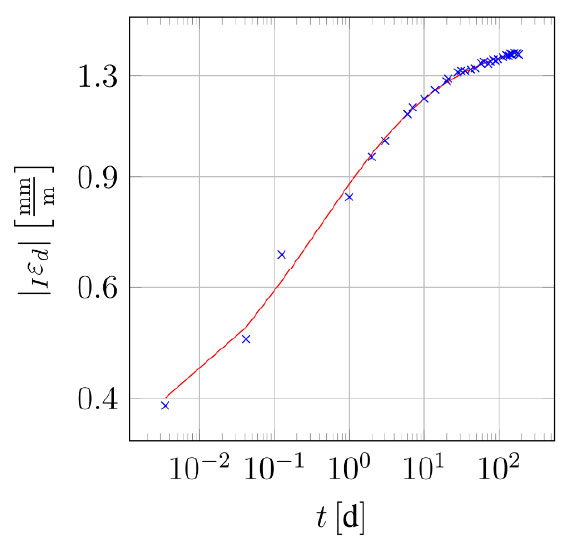
- M. Hinze, S. Xiao, A. Schmidt & W. Nowak: Experimental Evaluation and Uncertainty Quantification for a Fractional Viscoelastic Model of Salt Concrete. Mech. Time-Depend. Mater. (2022), DOI 10.1007/s11043-021-09534-9